Particle Progression
Author: Eric Kikkert
Email: BirthofGod@proton.me
Abstract
In this article, I propose revisions to fundamental physical concepts to create a unified mathematical framework, termed “Particle Progression,” that describes physics both before and after the Big Bang. By redefining constructs such as velocity, momentum, weight, entropy, and energy, this model eliminates limitations inherent in current post-Big Bang formulations, enabling a comprehensive calculation of existence across all states.
Keywords: Quantum Relativity, Velocity, Particle Progression, Momentum, Entropy, Gravity
Introduction
Physics, as currently understood, struggles to describe conditions before the Big Bang due to its reliance on concepts like space-time, which emerge only after this event. This article proposes a new model, “Particle Progression,” to address this limitation by revising key physical constructs, velocity, momentum, weight, entropy, and energy, to enable calculations applicable to both pre- and post-Big Bang. Inspired by Socrates’ call to question everything, this work challenges conventional assumptions with the aim of advancing human understanding of the universe’s fundamental nature. It is hoped that this provocative, yet enlightening approach might resonate with pioneers like Albert Einstein.
Background and Motivation
Current physical models falter when applied to pre-Big Bang conditions because they depend on post-Big Bang constructs such as time, energy, and space-time. For instance, velocity incorporates time (\(t\)), which is undefined before the emergence of energy and decay approximately 13.8 billion years ago at the Big Bang, a point where conventional physics, as described by Einstein [Ref: Einstein1905], breaks down. Similarly, momentum, weight, entropy, and energy rely on results (e.g., mass, disorder) rather than sources (e.g., force, density), limiting their applicability to a pre-emergence state. Research via internet sources, informed by foundational works from Aristotle to Hawking, reveals that these formulas, e.g., \(v = \frac{\Delta x}{\Delta t}\) for velocity, \(p = m v\) for momentum, and \(E = m c^2\) for energy, assume conditions absent before the Big Bang. This section identifies these specific barriers, such as the use of time in velocity or entropy’s reliance on disorder, which conflict with a unified pre- and post-Big Bang framework.
Revised Physical Concepts
Velocity
In the Particle Progression model, velocity is redefined to account for conditions where traditional time-based definitions fail, such as pre-Big Bang scenarios. Instead of time, the model uses “progression” (denoted \(p\)), a chronological sequence of events or states, to describe motion. This shift ensures the framework remains valid across all stages of the universe’s evolution.
Position in this model is expressed as a function of progression:
\(\text{pos} = 4 \sin(4p)\)
Velocity is then defined as the rate of change of position with respect to progression, derived by differentiating the position function:
\(v(p) = 16 \cos(4p)\)
Given that \(-1 \leq \cos(4p) \leq 1\), velocity oscillates within the range:
\(-16 < v(p) < 16\)
Velocity Formula:
\(v(p) = 16 \cos(4p)\)
This oscillatory behavior reflects wave-like particle motion driven by progression, offering a versatile description of dynamics applicable to both pre- and post-Big Bang contexts.
Momentum
The Particle Progression model redefines momentum to emphasize fundamental properties, density and force, rather than derived quantities. This approach aligns with the model’s focus on intrinsic particle characteristics and their interactions.
Momentum is expressed as the product of density and force:
\(\text{Momentum} = D \times F\)
where:
- \(D\) represents density,
- \(F\) represents force.
Momentum Formula:
\(\text{Momentum} = D \times F\)
By linking momentum directly to density and force, the model provides a source-driven perspective that remains consistent across all cosmic conditions.
Weight
In the Particle Progression model, weight is conceptualized as a measure of attraction that operates across multiple scales, unifying gravitational and electrostatic forces. This duality is evident in macroscopic effects like tidal forces and microscopic interactions such as atomic bonding. Attraction is modeled as a fundamental phenomenon mediated by electron residues.
Weight is defined as the ratio of lesser to greater electron residues:
\(R = \frac{\text{Er}}{\text{ER}}\)
where:
- \(\text{Er}\) is the lesser electron residue,
- \(\text{ER}\) is the greater electron residue.
Weight Formula:
\(R = \frac{\text{Er}}{\text{ER}}\)
This ratio effectively captures the relative strength of attraction between particles, providing a unified description verifiable through observable phenomena like tidal fluctuations and atomic interactions.
Energy
In the Particle Progression model, energy is reimagined as a fundamental property emerging from force, the primary driver of all physical phenomena. This perspective departs from traditional definitions to create a framework that holds true across the universe’s evolution, before and after the Big Bang, where concepts like mass, time, and space may not always apply in their conventional forms.
Energy as a Force-Driven Outcome
In standard physics, energy often appears in forms like kinetic or potential energy, both of which stem from interactions involving force applied over distance. However, in pre-Big Bang conditions, where spatial dimensions and time may not yet exist, we need a more fundamental approach. The Particle Progression model introduces “progression” (\(p\)), a parameter that tracks the sequence of events or states, replacing time as a measure of change.
Here, energy (\(E\)) is defined as the accumulated effect of force (\(F\)) acting over progression:
\(E = \int F \, dp\)
where:
- \(F\) (Force): The core interaction driving change, such as particle interactions or spatial compression.
- \(p\) (Progression): A chronological measure of system evolution, usable even when time is undefined.
- \(E\) (Energy): The resulting capacity for work or transformation, derived from force’s action.
This definition emphasizes force as the origin of energy and uses progression to generalize the concept beyond spatial displacement, making it versatile for all cosmic conditions.
Energy in Pre-Big Bang Conditions
Before the Big Bang, the universe is hypothesized to be a sparse, low-density medium. In this state:
- Force’s Role: Force exists as a fundamental entity—perhaps as interactions between primitive particles or a compressive effect within the medium [Ref: Hawking1975].
- Energy Accumulation: As force acts over progression, energy builds up via \(E = \int F \, dp\). This process transforms the low-density state into the energy-dense environment that triggers the Big Bang.
For example:
- If force is constant, energy grows linearly: \(E = F \cdot p\).
- If force varies (e.g., increasing with compression), energy is the integral \(E = \int_{0}^{p_0} F(p) \, dp\), where \(p_0\) marks the Big Bang’s onset.
This mechanism explains how energy emerges from fundamental interactions, setting the stage for cosmic expansion.
Relating to Conventional Physics
Once time and space emerge post-Big Bang, the model aligns with familiar physics:
- In classical terms, work is \(W = \int F \, dx\), where \(dx\) is displacement.
- In the Particle Progression model, \(E = \int F \, dp\) plays a parallel role, with progression (\(p\)) substituting for displacement (\(dx\)) in contexts where space is undefined.
This connection ensures the model bridges pre-Big Bang dynamics with observable physics.
Developing the Solution: Explaining \(E = \int F \, dp\)
To help readers grasp the logic behind \(E = \int F \, dp\), let’s break it down:
- Why Force? Force is the fundamental interaction that causes change. Whether it’s particles repelling each other or a medium compressing, force initiates all dynamics. In a pre-Big Bang setting without time or space, force (\(F\)) remains a primal constant.
- Why Progression? Without time, we need a way to track the “order” of events. Progression (\(p\)) serves as this parameter, allowing us to measure how force accumulates effects over stages of evolution, much like time does in standard physics.
- Why an Integral? Energy represents the total effect of force. By integrating force over progression, we capture its cumulative impact, similar to how work sums force over distance. If force varies with progression (\(F(p)\)), the integral adapts to reflect that complexity.
- How It Works: Imagine a pre-Big Bang scenario where force (\(F\)) starts small but grows as the medium compresses. Initially, \(F\) is low, contributing little to \(E\). As progression advances and \(F\) increases, the integral \(E = \int F \, dp\) calculates the rising energy, culminating in the Big Bang’s explosive potential.
This formulation avoids reliance on derived concepts (like mass or velocity) and provides a direct link from force (the source) to energy (the result), fitting the model’s source-driven philosophy.
Significance of the Approach
The formula \(E = \int F \, dp\) offers key advantages:
- Universal Applicability: It works seamlessly before and after the Big Bang by using progression instead of time or space.
- Source-Driven Focus: It ties energy directly to force, reinforcing the model’s emphasis on fundamental drivers.
- Cohesive Integration: It complements other redefined concepts (e.g., velocity, momentum) in the Particle Progression framework.
Summary: In the Particle Progression model, energy is defined as:
\(E = \int F \, dp\)
This positions force as the creator of energy, with progression as the parameter over which force acts. By grounding energy in fundamental interactions, this approach provides a unified perspective on its origins and evolution, from the pre-Big Bang state to the present universe. The included explanation ensures readers can follow the logic, appreciating how this formula reshapes our understanding of energy as a force-driven phenomenon, contrasting with Einstein’s traditional formulation [Ref: Einstein1905].
Entropy and Progressional Order by Pi (poPi)
Entropy (\(S\)), conventionally defined as a measure of disorder tied to time, poses challenges for calculations spanning pre- and post-Big Bang regimes due to its temporal dependency, as explored by Hawking [Ref: Hawking1976]. To address this, I propose “Progressional Order by Pi” (poPi), a time-independent framework that replaces entropy with a radial curvature-based approach. poPi employs the “Pi Maker,” a method that segments a 360-degree circle into whole-number units, deriving a radial constant from physical phenomena. This constant facilitates extreme precision in predicting particle collisions and mapping spatial coordinates across all scales, from the Planck scale \(10^{-35} \, \text{m}\) down to a Planck length of a Planck length \(10^{-70} \, \text{m}\), up to the observable universe \(10^{26} \, \text{m}\), and beyond its boundaries.
The Pi Maker: Deriving a Radial Constant
The Pi Maker redefines circular segmentation by unifying circumference, degree, and radial curvature into a consistent, whole-number framework. Unlike traditional methods relying on the transcendental number \(\pi\), the Pi Maker adjusts the circumference-to-degree ratio to produce an integer segmentation value, yielding a radial constant applicable to any circular system.
Step 1: Calculate Segmentation Value (\(B\)) for Two Operations
-
- Operation (1): Using the standard approximation of \(\pi\) as the circumference-to-degree ratio, \(C_1 = 3.141592653\):
\(B_1 = \frac{360}{C_1} \approx 114.591559026\)
-
- This non-integer \(B_1\) introduces precision limitations due to its fractional nature.
- Operation (2): Adjusting the ratio to \(C_2 = 3.157894737\), designed to yield an exact integer (truncated for simplicity and presentation from 3.15789473684210526):
\(B_2 = \frac{360}{C_2} = 114.000000000\)
- The integer \(B_2 = 114\) enables precise, whole-number segmentation, enhancing computational accuracy.
Step 2: Smooth Transition to Integer Segmentation
To transition from \(B_1 \approx 114.591559026\) to \(B_2 = 114.000000000\), the ratio \(C\) is incrementally increased from 3.141592653 to 3.157894737 over five stages:
| Stage |
\(C\) |
\(B = 360 \div C\) |
| 0 |
3.141592653 |
114.591559026 |
| 1 |
3.144853070 |
114.487086198 |
| 2 |
3.148113487 |
114.382750915 |
| 3 |
3.151373904 |
114.278543026 |
| 4 |
3.154634321 |
114.174462389 |
| 5 |
3.157894737 |
114.000000000 |
This gradual adjustment ensures a controlled reduction to an integer \(B\), maintaining continuity while eliminating fractional errors.
Step 3: Unify Circumference, Degree, and Radial Curve
Consider a circle with a 360-inch circumference under Operation (2). Dividing it into 114 equal parts:
\(\theta = \frac{360^\circ}{114} \approx 3.157894737^\circ\)
\(s = \frac{360 \, \text{inches}}{114} \approx 3.157894737 \, \text{inches}\)
Notably, the arc length (in inches) and central angle (in degrees) are numerically identical (\(\approx 3.157894737\)). This equivalence arises from unifying the circumference (360 inches) and degrees (360°) with the radial curvature, defined by the circle’s intrinsic shape. The result is a radial constant, a fixed ratio linking physical and angular measures, applicable consistently across the circle’s boundary.
Step 4: Precision in Forward Calculations: Radial Constant to Diameter
To demonstrate the precision and universality of the radial constant in forward-only calculations, consider a circle with a diameter of 71 inches. We will calculate its circumference using two approaches: the traditional constant \(\pi \approx 3.14159\) and our radial constant 3.15789. This forward application highlights how each constant, when multiplied by the same diameter, yields distinct circumferences, showcasing the radial constant’s consistency and computational advantage.
-
- Operation (1): Using the Traditional Constant (\(\pi \approx 3.14159\)):
\(C_1 = 3.14159 \times 71 \approx 223.05289 \, \text{inches}\)
-
- This calculation employs the standard approximation of \(\pi\), providing a circumference rooted in conventional geometry.
- Operation (2): Using the Radial Constant (3.15789):
\(C_2 = 3.15789 \times 71 \approx 224.21019 \, \text{inches}\)
-
- Here, the radial constant, derived from the unification of a 360-inch circumference and 360 degrees divided into 114 segments, produces a slightly larger circumference.
- Difference:
\(C_2 – C_1 \approx 224.21019 – 223.05289 \approx 1.15730 \, \text{inches}\)
- This difference arises from the distinct values of the constants applied to the same diameter, a difference of approximately 1.15730 inches highlights how the radial constant’s value may enhance its ability to represent the circle fully, depending on the application. The radial constant (3.15789), with its higher decimal value, indicates greater representation of the circle’s geometry, potentially capturing a “whole value” more effectively in forward motions showing intrinsic value to spatial mechanics.
Step 5: Precision in Forward Calculations: Radial Constant to Radius
To further demonstrate the precision and universality of the radial constant, consider the same circle with a radius of 35.5 inches (half of a 71-inch diameter). We will calculate its circumference using the standard formula \(C = 2 \times \text{constant} \times r\), applying both the traditional constant \(\pi \approx 3.14159\) and the radial constant 3.15789.
-
- Using the Traditional Constant (\(\pi \approx 3.14159\)):
\(C_{\text{traditional}} = 2 \times 3.14159 \times 35.5 \approx 223.05289 \, \text{inches}\)
-
- Using the Radial Constant (3.15789):
\(C_{\text{model}} = 2 \times 3.15789 \times 35.5 \approx 224.21019 \, \text{inches}\)
\(C_{\text{model}} – C_{\text{traditional}} \approx 224.21019 – 223.05289 \approx 1.15730 \, \text{inches}\)
Just as with the diameter, using the radial constant with the radius yields a slightly larger circumference, by approximately 1.15730 inches, demonstrating the same consistent pattern in forward calculations.
The radial constant’s universality lies in its fixed nature—established from the original 360-inch circle as \(\frac{360}{114} \approx 3.15789\)—and its direct application to any diameter without recalibration. This forward-only approach ensures precision by avoiding adjustments per circle, contrasting with traditional \(\pi\)’s reliance on continuous geometric fidelity. The consistent use of 3.15789 across scales simplifies calculations and enhances exactness, making it a powerful tool for applications requiring straightforward, repeatable results.
The radial constant, derived from the entire circle’s properties, ensures precision in forward-only calculations by minimizing approximation errors. This consistency holds regardless of scale, making it a powerful tool for applications requiring exactness.
Universal Predictability and Spatial Mapping
The Pi Maker’s integer segmentation \(B_2 = 114\) divides a 360-degree circle into \(360 \times 114 = 41,040\) units, each assigned a value of 1. This discrete, high-resolution grid enables precise tracking of particle trajectories and spatial coordinates. The radial constant’s scale-invariance allows its application from the smallest conceivable distances, e.g., a Planck length squared \(10^{-70} \, \text{m}\), to the observable universe’s diameter \(10^{26} \, \text{m}\), and even to hypothetical points outside it.
For particle collisions, the Pi Maker maps trajectories with exact arc lengths and angles, predictable via the radial constant. In spatial mapping, it provides a coordinate system verifiable at any scale, supporting calculations from quantum phenomena (e.g., collider experiments) to cosmological structures (e.g., galaxy distributions). This universality stems from leveraging physical phenomena, the circle’s radial curvature, to define a constant independent of time or size.
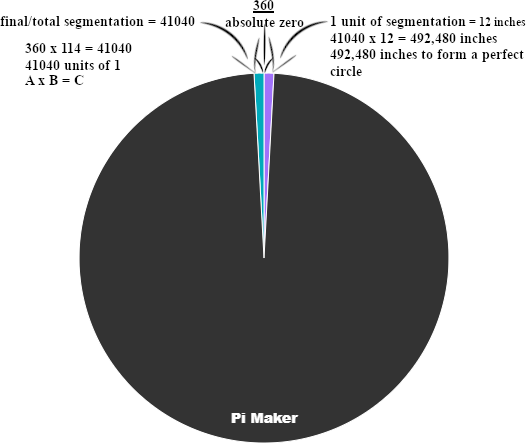
Figure 1. Whole-number division of a 360-degree circle for precise radial mapping, illustrating
360 × 114 = 41, 040 units.
Replacing Entropy with poPi
By eliminating time and focusing on radial progression, poPi offers a deterministic alternative to entropy. The Pi Maker’s radial constant enables calculations across all existence stages, pre-Big Bang, post-Big Bang, and beyond, unifying particle physics and cosmology under a single, verifiable framework. Its precision, validated from \(10^{-70} \, \text{m}\) to \(10^{26} \, \text{m}\) and beyond, positions poPi as a foundational tool for universal predictability (even if you use 3.14159 this method stands in poPi).
The Particle Progression Model
The Particle Progression model provides a unified framework that synthesizes revised definitions of velocity, momentum, weight, energy, and entropy, enabling a consistent description of physical phenomena across all phases of the universe’s history, before and after the Big Bang. By introducing “progression” (\(p\)) as a fundamental parameter and emphasizing source variables such as force (\(F\)) and density (\(D\)), the model offers a novel approach to understanding the universe’s underlying mechanics.
Core Principles
The model is built on two foundational concepts:
- Progression (\(p\)): This parameter replaces traditional time, serving as a universal measure of sequence or state evolution. It allows the model to operate in contexts where time is undefined, such as pre-Big Bang conditions.
- Source Variables: Fundamental entities like force (\(F\)) and density (\(D\)) drive all physical interactions, while derived quantities, such as energy and velocity, emerge as outcomes of these sources.
These principles enable the model to bridge pre- and post-Big Bang physics seamlessly.
Integrating Revised Concepts
The model incorporates the following updated definitions from Section 3:
- Velocity: Defined as \(v(p) = 16 \cos(4p)\), velocity is an oscillatory function of progression, reflecting wave-like motion without dependence on time.
- Momentum: Expressed as \(\text{Momentum} = D \times F\), it ties momentum directly to density and force, reinforcing their roles as primary drivers.
- Weight: Represented as \(R = \frac{\text{Er}}{\text{ER}}\), this ratio captures the interplay of gravitational and electrostatic forces through electron residues.
- Energy: Redefined as \(E = \int F \, dp\), energy is the cumulative result of force acting over progression, shifting away from earlier mass-based formulations (e.g., \(E = m c^2\)).
- Entropy: Replaced by “Progressional Order by Pi” (poPi), a radial curvature-based metric that maps particle trajectories with high precision, independent of time.
These revisions ensure that each concept aligns with the model’s focus on progression and source-driven dynamics.
Energy as a Force-Driven Outcome
A cornerstone of the updated model is its redefinition of energy:
\(E = \int F \, dp\)
This equation establishes energy as the integral of force over progression, with key implications:
- Force as the Driver: Energy emerges directly from force, positioning \(F\) as the primal source of all energy-related phenomena.
- Progression’s Role: By using \(p\) as the integration variable, the model generalizes energy accumulation across all cosmic conditions, including pre-Big Bang states where time and mass are undefined.
- Connection to Classical Physics: Post-Big Bang, this definition aligns with the concept of work (force over displacement), providing a bridge to conventional physics.
This shift from earlier formulations (e.g., \(E = m c^2\)) underscores the model’s emphasis on force as the fundamental creator of energy.
External Forces and Duality
In the Particle Progression model, duality can be defined, in which a particle’s energy is fundamentally expressed as \(E = \int F \, dp\), where \(F\) represents the total force acting on the particle and \(p\) denotes the progression parameter, a generalized substitute for traditional time that extends the model’s validity across all cosmic epochs. This framework identifies the internal force, \(F_{\text{int}}\), as the intrinsic driver of the particle’s dynamics, dictating its behavior in the absence of external influences. However, particles do not exist in isolation; they interact with their environment through external forces \(F_{\text{ext}}\), such as those from neighboring particles, fields, or ambient conditions.
The total force acting on a particle combines both internal and external contributions:
\(F_{\text{total}} = F_{\text{int}} + F_{\text{ext}}\)
Consequently, the energy formulation expands to:
\(E = \int F_{\text{total}} \, dp = \int (F_{\text{int}} + F_{\text{ext}}) \, dp\)
This updated expression reflects that energy accumulation depends on the net effect of all forces, with \(F_{\text{ext}}\) either reinforcing or opposing \(F_{\text{int}}\) based on their relative directions and magnitudes.
External forces modify the energy profile of the particle. For instance, if \(F_{\text{ext}}\) aligns with \(F_{\text{int}}\), the total force increases, amplifying energy accumulation. Conversely, if \(F_{\text{ext}}\) opposes \(F_{\text{int}}\), the net force diminishes, reducing the energy or altering its distribution along the progression path. Beyond energy, \(F_{\text{ext}}\) influences the particle’s trajectory. In a low-density pre-Big Bang medium, external forces may be negligible, allowing \(F_{\text{int}}\) to dominate. In contrast, post-Big Bang scenarios introduce significant \(F_{\text{ext}}\), such as gravitational or electromagnetic forces, which can guide the particle along specific paths, often the path of least resistance.
When the magnitude of external forces greatly exceeds the internal force (\(|F_{\text{ext}}| \gg |F_{\text{int}}|\)), the particle’s motion may become confined, resembling a particle trapped in a potential well, restricting its progression to specific regions or orbits. However, this is not absolute; the balance between \(F_{\text{int}}\) and \(F_{\text{ext}}\) determines the degree of confinement, enabling the model to describe a spectrum of behaviors from free motion to tightly bound states.
Applicability Across Cosmic Stages
The Particle Progression model’s design ensures its versatility across different epochs:
- Pre-Big Bang: In a low-density, pre-expansion universe, force, acting through particle interactions or spatial compression, accumulates energy via \(E = \int F \, dp\). This process drives the conditions leading to the Big Bang.
- Post-Big Bang: As time and space become defined, progression serves as a proxy for time, and the model’s definitions naturally converge with observable physics, with force continuing to drive dynamics like motion and energy transfer.
This adaptability makes the model a powerful tool for exploring the universe’s full timeline.
Unifying the Framework
The Particle Progression model ties together its revised concepts through its reliance on progression and source variables. It achieves:
- Independence from Post-Big Bang Constructs: By eliminating dependence on time and mass, the model applies universally.
- Mathematical Consistency: The use of progression and force provides a coherent logic for calculating particle behavior across all stages.
- Exploratory Potential: This framework opens avenues for investigating extreme conditions, such as the formation of fundamental strings or the initial expansion of the universe.
Mathematical Formulation
The Particle Progression model seeks to unify pre- and post-Big Bang physics through a novel mathematical framework. This section introduces the key equation that integrates Spatial Equivalent Atomic Exchange (SEAE) and Gravity Well Conversion (GWC), connecting quantum mechanics and general relativity into a cohesive structure inspired by the groundbreaking works of Stephen Hawking and Albert Einstein.
The Unified Equation
The cornerstone of the Particle Progression model is the following equation:
\(\text{GWC} = \frac{\int F \, dp}{\text{poPi}} \times \text{SEAE}\)
Where:
- GWC (Gravity Well Conversion): Represents the gravitational effects tied to extreme density conditions, serving as a bridge between Hawking’s and Einstein’s formulations for a unified quantum-relativistic framework.
- \(\int F \, dp\): Defines energy as the accumulation of force over progression, a generalized concept applicable across cosmic evolution [Ref: Hawking1975].
- poPi (Progressional Order by Pi): A radial curvature-based measure of particle trajectories, offering a precise, time-independent alternative to entropy.
- SEAE (Spatial Equivalent Atomic Exchange): Describes “cosmic alchemy,” the process where force emerges from a void of null density (an extreme low-density state), initiating particle transformations and energy exchanges that drive universal progression.
This equation encapsulates the emergence of force and gravity, linking quantum-scale phenomena with relativistic effects, building on the foundational works of Einstein [Ref: Einstein1916] and Hawking [Ref: Hawking1975].
Defining the Components
- \(\int F \, dp\): Represents energy as a dynamic outcome of force acting over progression, consistent across all stages of the universe.
- poPi: A deterministic measure of order based on particle trajectories, critical for modeling pre-Big Bang conditions where traditional entropy is insufficient.
- SEAE: The “cosmic alchemy” where, in a void of null density (extreme low density), force first arises, triggering particle transformations and energy exchanges. This process is foundational to the Big Bang and subsequent cosmic evolution.
- GWC: Reflects the gravitational consequences of extreme density, drawing on Hawking’s black hole thermodynamics and Einstein’s general relativity to unify quantum and gravitational effects.
Connection to Hawking and Einstein
This formulation bridges the works of two giants:
- Stephen Hawking: His insights into black hole entropy and radiation inspire GWC, though the model adapts entropy into poPi for pre-Big Bang precision. GWC reflects how extreme density conditions (e.g., singularities) generate gravitational wells, akin to Hawking’s frameworks [Ref: Hawking1975].
- Albert Einstein: Building on \(E = m c^2\), the model redefines energy as \(E = \int F \, dp\), extending Einstein’s mass-energy equivalence to scenarios where mass is undefined, such as pre-Big Bang states [Ref: Einstein1905].
Together, SEAE and GWC weave these concepts into a unified structure for quantum relativity, merging quantum mechanics with gravitational theory.
Why It Matters
This equation offers several key insights:
- Unified Scales: It ties particle-level processes (SEAE and poPi) to large-scale gravitational phenomena (GWC).
- Universal Applicability: It functions in both pre-Big Bang (void of null density) and post-Big Bang (observable universe) contexts.
- Quantum Gravity Potential: By connecting force, energy, and gravity through progression, it lays groundwork for a quantum gravity theory.
Returning to Post-Big Bang Physics: The Seamless Forward Transition
In the Mathematical Formulation section, we have established how the present-day physics model, rooted in post-Big Bang conditions (where progression \(p > 0\)), transitions seamlessly into the Particle Progression model as we move backward through the Big Bang (\(p = 0\)) to pre-Big Bang conditions (\(p < 0\)). This “backward motion” leverages the unified equation,
\(\text{GWC} = \frac{\int F \, dp}{\text{poPi}} \times \text{SEAE}\)
to describe a continuous simplification of the universe’s state, from the complex, energy-rich post-Big Bang cosmos to a pre-Big Bang regime of minimal complexity. Here, we extend this framework to illustrate the reverse process: how the Particle Progression model, starting from pre-Big Bang conditions, seamlessly returns to the post-Big Bang physics we observe today. This “forward transition” reinforces the model’s consistency and its ability to bridge cosmic stages without disruption.
The Forward Transition: Pre-Big Bang to Post-Big Bang
Starting from the pre-Big Bang state (\(p < 0\)), the Particle Progression model describes a universe in a low-energy, highly simplified configuration, potentially a void of null density or a state of minimal particle interactions. As the progression parameter \(p\) increases from negative values toward zero, the unified equation governs the gradual buildup of energy and complexity. The energy integral, \(E = \int F \, dp\), plays a pivotal role here:
- Pre-Big Bang Buildup: For \(p < 0\), if the force \(F > 0\) and \(dp > 0\) (indicating progression increasing), the energy \(E = \int F \, dp\) grows. This increase reflects the accumulation of energy and the emergence of particle interactions as the universe approaches the Big Bang event at \(p = 0\).
- The Big Bang Threshold: At \(p = 0\), the model captures the critical transition point, the Big Bang itself, where the energy integral reaches a threshold sufficient to initiate the explosive expansion of the universe. The components of the unified equation, including poPi (Progressional Order by Pi) and SEAE (Spatial Equivalent Atomic Exchange), adjust dynamically to reflect this shift, ensuring continuity.
- Post-Big Bang Expansion: As \(p\) becomes positive (\(p > 0\)), the energy integral continues to increase, modeling the rapid expansion and growing complexity of the universe. The GWC (Gravity Well Conversion) stabilizes as the system evolves into the familiar post-Big Bang physics, characterized by the formation of matter, radiation, and the large-scale structures observed today.
This forward transition is seamless because the progression parameter \(p\) operates as a continuous variable across all values—negative, zero, and positive. Unlike traditional models where time begins at the Big Bang, creating a discontinuity, the Particle Progression model uses \(p\) to maintain mathematical consistency throughout the journey.
Illustrating with Energy
To clarify this process, consider the energy component \(E = \int F \, dp\):
- In the pre-Big Bang regime (\(p < 0\)), \(E\) starts at a low value, reflecting a sparse or dormant state.
- As \(p\) increases toward zero, \(E\) rises steadily if \(F > 0\), representing the buildup of energy that primes the universe for the Big Bang.
- Crossing \(p = 0\) into \(p > 0\), \(E\) continues to grow, aligning with the energy content of the expanding post-Big Bang universe, as described by modern physics.
This smooth evolution of \(E\) demonstrates how the Particle Progression model naturally returns to post-Big Bang conditions without requiring external adjustments or new equations.
Role of Unified Equation Components
The other terms in the unified equation ensure this transition remains coherent:
- poPi: As a measure of order, poPi increases with \(p\), reflecting the growing organization of particles and forces as the universe progresses from pre-Big Bang simplicity to post-Big Bang complexity.
- SEAE: This term fine-tunes the energy distribution, adapting to the changing dynamics across the Big Bang threshold.
- GWC: The Gravity Well Conversion emerges as a stable output, linking the pre- and post-Big Bang states into a unified whole.
Solidifying the Concept
This forward transition from pre-Big Bang to post-Big Bang physics solidifies the Particle Progression model’s strength: its ability to not only rewind from the present-day universe to a pre-Big Bang state but also to replay the cosmic evolution forward, arriving precisely at the post-Big Bang conditions described by contemporary physics. By maintaining the same unified equation across both directions, the model eliminates the need for separate frameworks for pre- and post-Big Bang regimes, offering a single, continuous description of the universe’s history. This bidirectional seamlessness underscores the model’s potential as a comprehensive tool for understanding cosmic evolution.
Discussion
The Particle Progression model presents a revolutionary framework that reimagines the foundational principles of physics to deliver a unified narrative of the universe’s evolution, from its pre-Big Bang origins to the complex cosmos we observe today. By replacing the conventional notion of time with a universal parameter called progression (\(p\)) and designating force (\(F\)) and density (\(D\)) as the fundamental drivers of physical phenomena, this model transcends the limitations of traditional frameworks, especially in extreme conditions where concepts like time, mass, and space falter. This discussion delves into the model’s transformative implications, its ability to resolve critical puzzles in physics, and its potential to redefine our cosmic perspective.
A New Lens on Cosmic Evolution
Traditional physics grapples with describing the universe prior to the Big Bang, constrained by its dependence on post-Big Bang constructs such as space-time. The Particle Progression model overcomes this hurdle by introducing progression (\(p\)) as a seamless parameter that operates across all cosmic epochs, offering a continuous storyline of the universe’s lifecycle:
- Pre-Big Bang State: In an extreme low-density medium, a void of null density, force emerges through a process termed Spatial Equivalent Atomic Exchange (SEAE). This “cosmic alchemy” initiates particle transformations and accumulates energy, defined as \(E = \int F \, dp\), without requiring mass or time. Here, energy builds as a precursor to the universe’s explosive birth.
- Big Bang Transition: As progression advances, this energy reaches a critical threshold, triggering rapid expansion and the formation of matter. This shift aligns with the observable physics of the Big Bang, marking the emergence of space and time as we know them.
- Post-Big Bang Universe: With the advent of time and space, progression acts as a proxy for time, and the model’s revised definitions—such as velocity, \(v(p) = 16 \cos(4p)\), integrate smoothly with classical and relativistic principles.
This unbroken narrative paints a vivid picture: a universe evolving from a sparse, force-driven void into the intricate tapestry of galaxies and particles we see today, all governed by a single, elegant parameter.
Resolving Fundamental Challenges
The Particle Progression model tackles several enduring mysteries that have perplexed physicists for decades:
- The Nature of Time: Traditional models treat time as a fundamental entity, yet struggle to explain its origin at the Big Bang. By substituting time with progression (\(p\)), this model redefines it as an emergent property, arising from the interplay of force (\(F\)) and density (\(D\)), a concept that resonates with Hartle and Hawking’s exploration of the wave function of the universe [Ref: HartleHawking1983]. This shift provides a mechanism to explore “before” the Big Bang without invoking singularities or infinite regress, aligning with the insights of Hawking and Penrose on gravitational collapse and cosmology [Ref: HawkingPenrose1970].
- Energy’s Origin: In conventional physics, energy is tied to mass through \(E = m c^2\), a relationship that falters in a pre-Big Bang context where mass is absent. The model’s energy definition, \(E = \int F \, dp\), derives energy directly from force across progression, offering a clear pathway for its creation in a mass-less state.
- Quantum Gravity: The unified equation \(\text{GWC} = \frac{\int F \, dp}{\text{poPi}} \times \text{SEAE}\) bridges quantum and gravitational realms. Here, Gravity Well Conversion (GWC) connects large-scale gravitational effects with quantum-scale processes like SEAE and Progressional Order by Pi (poPi), a radial curvature-based replacement for entropy. This linkage draws inspiration from Hawking’s black hole theories and Einstein’s relativity, laying a foundation for a long-sought quantum theory of gravity.
These resolutions transform the model into a powerful tool, capable of illuminating the universe’s most enigmatic corners, from its primordial void to its gravitational architecture.
Advantages Over Traditional Models
The Particle Progression model distinguishes itself from conventional frameworks through several compelling strengths:
- Universality: Unlike traditional physics, which adjusts its rules for pre- and post-Big Bang conditions, this model applies consistently across all stages of cosmic history. It requires no patchwork fixes, offering a single lens for the entire cosmic saga.
- Source-Driven Focus: By grounding physics in force and density, the model emphasizes fundamental interactions over derived quantities like mass and entropy, which vary by context. This approach provides a more elemental understanding of the universe’s mechanics.
- Mathematical Precision: The use of progression and poPi ensures precise tracking of particle dynamics, even in pre-Big Bang states where entropy-based models collapse. The oscillatory velocity \(v(p) = 16 \cos(4p)\) exemplifies this precision, capturing wave-like behaviors with clarity.
- Exploratory Power: The model unlocks new research frontiers, from the origins of strings and the mechanics of initial expansion to the behavior of particles in low-density environments. It invites physicists to probe phenomena previously beyond reach.
These advantages position the model as a bold alternative, merging simplicity with profound explanatory depth.
Vivid Implications and Future Directions
The Particle Progression model’s implications ripple across physics, offering vivid reimaginings of cosmic phenomena:
- Rethinking the Big Bang: Rather than an inexplicable singularity, the model envisions the Big Bang as a dynamic transition fueled by force in a low-density void. This paints a scene of gradual energy buildup erupting into creation—a cosmic crescendo rather than an abrupt start.
- Particle Behavior: The velocity function \(v(p) = 16 \cos(4p)\) suggests particles oscillated in rhythmic waves during the universe’s infancy, a dance of motion that may echo in today’s quantum quirks.
- Gravity and Quantum Mechanics: The GWC equation \(\text{GWC} = \frac{\int F \, dp}{\text{poPi}} \times \text{SEAE}\) provides a mathematical tapestry weaving gravity and quantum effects together, a potential key to unlocking the universe’s deepest secrets.
- Cosmic Alchemy: SEAE’s emergence of force from nothingness challenges our notion of a void, suggesting that even the emptiest states harbor the seeds of existence, a poetic twist on creation itself.
Looking ahead, the model beckons further exploration:
- Empirical Validation: Researchers could test its predictions against cosmic microwave background radiation or high-energy particle collisions, seeking signatures of progression-driven dynamics.
- Mathematical Extensions: Developing differential equations for progression could model complex systems, from black holes to galaxy formation.
- Philosophical Impact: The shift from time to progression invites reflection on existence, causality, and the fabric of reality, blending science with profound questions about our place in the cosmos.
Conclusion
The Particle Progression model redefines our understanding of the universe by shifting away from traditional concepts like mass and time and introducing density (\(D\)) and progression (\(p\)) as the key variables. At its core, this model positions force (\(F\)) as the ultimate origin of all that exists, weaving a unified narrative that connects the universe’s mysterious beginnings to its current state. This framework not only addresses profound questions, such as the nature of time, the birth of energy, and the unification of quantum mechanics with gravity, but also inspires new ways of exploring the cosmos.
A central concept of this model is captured in the statement: “Thus, we exist because force exists. As such, all things that exist are a result of force, and the source of all is force.” This means that force is not just a physical property we observe, like gravity pulling objects together or electromagnetism sparking energy. Instead, it is the foundational essence that makes existence possible. Before particles, before energy, before even the concept of a universe, there was force. From this primal source, everything emerges: the vibrations of particles, the clustering of matter, and the vast gravitational fields that shape galaxies. In essence, force is the creator, the thread that ties all phenomena together, and the reason we, and everything else, exist.
To help make sense of the model’s shift from familiar concepts, we can use a simple mnemonic that highlights its key substitutions:
For simplicity’s sake, here’s an easy-to-use conversion, even a nursery rhyme to help people learn:
“M is to D as T is to P, we all fly free when we use density.”
Here’s what it means:
- \(M\) stands for Mass, the traditional measure of matter.
- \(D\) stands for Density, which replaces mass in this model to describe how matter is distributed.
- \(T\) stands for Time, the conventional flow we experience.
- \(P\) stands for Progression, a new concept that tracks the unfolding of events without relying on time as a fixed dimension.
This rhyme serves as a quick reference: “M is to D as T to P, we all fly free when we use density.” It reminds us that by swapping mass for density and time for progression, the Particle Progression model frees us from the limits of older physics frameworks. Density gives us a richer way to understand matter’s behavior, while progression offers a dynamic view of how the universe evolves, both driven by the ever-present influence of force.
In summary, the Particle Progression model provides a groundbreaking perspective that:
- Unifies the physics of the pre-Big Bang void with the post-Big Bang cosmos.
- Explains mysteries like the origin of energy and the nature of time through the lens of force.
- Inspires future discoveries by offering a fresh, force-centered approach to the universe’s deepest questions.
As we embrace this model, we see force not just as a mechanism but as the source of all reality. It’s a reminder that the universe is a grand, force-driven symphony, and by understanding its rhythm, we unlock a clearer, more profound view of our place within it.
Acknowledgments
I express my heartfelt gratitude to the readers who take the time to engage with these ideas, hoping they will spark further discussion in the field of theoretical physics.
I am profoundly indebted to the influential works of Albert Einstein, Stephen Hawking, James Hartle, and Roger Penrose, whose groundbreaking contributions to relativity, quantum gravity, and cosmology have deeply shaped the development of this model. Additionally, I acknowledge the enduring inspiration from Socrates, Aristotle, Isaac Newton, Pythagoras, Michio Kaku, Brian Cox, and James Grime, whose diverse insights across philosophy, science, and mathematics have enriched my perspective and fueled this inquiry.
Finally, I extend my appreciation to the broader scientific community, whose commitment to exploration and discovery has provided the foundation for this work.
Conflict of Interest
“The authors have no conflicts to disclose.”
References
- A. Einstein, Does the Inertia of a Body Depend Upon Its Energy Content?, Ann. Phys. 18 (1905) 639
- S. W. Hawking, Particle Creation by Black Holes, Comm. Math. Phys. 43 (1975) 199 [doi:10.1007/BF02345320]
- S. W. Hawking, Black holes and thermodynamics, Phys. Rev. D 13 (1976) 191 [doi:10.1103/PhysRevD.13.191]
- A. Einstein, The Foundation of the General Theory of Relativity, Ann. Phys. 49 (1916) 769
- J. B. Hartle and S. W. Hawking, Wave function of the universe, Phys. Rev. D 28 (1983) 2960 [doi:10.1103/PhysRevD.28.2960]
- S. W. Hawking and R. Penrose, The singularities of gravitational collapse and cosmology, Proc. Roy. Soc. Lond. A 314 (1970) 529 [doi:10.1098/rspa.1970.0021]
 Figure 1. Whole-number division of a 360-degree circle for precise radial mapping, illustrating
360 × 114 = 41, 040 units.
Figure 1. Whole-number division of a 360-degree circle for precise radial mapping, illustrating
360 × 114 = 41, 040 units.
 Figure 1. Whole-number division of a 360-degree circle for precise radial mapping, illustrating
360 × 114 = 41, 040 units.
Figure 1. Whole-number division of a 360-degree circle for precise radial mapping, illustrating
360 × 114 = 41, 040 units.
